Arbre De Dénombrement

1. Arbre de dénombrement ou arbre des possibles Nous avons déjà rencontré en classes de Seconde et et 1ère les arbres de dénombrement ou arbres des possibles, et les arbres pondérés de probabilités. Définition 1. On utilise un arbre de dénombrement ou un arbre des possibles, pour dénombrer toutes les issues possibles d'une expérience aléatoire. Ce qui correspondrait à des situations d' équiprobabilité. On calcule les probabilités comme le quotient des nombres d'issues favorables par le nombre d'issues possibles. Exemples Exercice résolu n°1. Une famille a deux enfants. On suppose qu'il y a autant de chances d'obtenir un garçon qu'une fille. Calculer la probabilité des événements « Obtenir une fille et un garçon » puis « Obtenir au moins une fille ». (On suppose qu'il n'y a pas de jumeaux). On appelle $F$ l'événement « obtenir une fille » et $G$ l'événement « obtenir un garçon » à chaque naissance: Fig. Arbre des possibles: Un chemin = Une issue L'univers associé à cette situation comporte quatre issues possibles.

Francais

Francais

Pour comprendre on va prendre un énoncé type: Enoncé: Une urne contient 7 boules numérotées de 1 à 7 on tire au hasard et successivement 3 boules de cette urne le tirage est avec remise, c'est à dire qu'on remet la boule une fois tirée. (voir exemple de tirage ci-dessous) Quel est alors le nombre de tirages possibles? il y a 7 choix possibles pour la première boule de même pour la seconde une fois la première boule sortie et de même pour la troisième boule. il y a dans ce cas 7 x 7 x 7 tirages possibles soit 343 tirages (le nombre de ramification à chaque branche est le même, il s'agit en fait du nombre de 3- listes dans un ensemble à 7 éléments -> bac++) le tirage est sans remise, c'est à dire qu'on ne remet pas la boule une fois tirée. (exemple de tirage ci-dessous) Il y a 7 sorties possibles pour la première boule, mais la seconde boule sera quant à elle tirée parmi les 6 restantes et la troisième parmi les 5 restantes. Le nombre de tirages est donc 7 x 6 x 5 = 210.

Vous pouvez vous désinscrire à tout moment. Vous trouverez pour cela nos informations de contact dans les conditions d'utilisation du site.  En soumettant ce formulaire, j'accepte que les informations saisies soient utilisées pour m'envoyer la newsletter

Compte tenu de ces événements, la règle de multiplication indique que la probabilité que les deux événements se produisent est trouvée en multipliant les probabilités de chaque événement. Construction du diagramme en arbre Mettre un point de départ à gauche. À partir de ce point, tracer autant de branches qu'il y a de résultats possibles pour la première étape. À partir de chaque nœud de la première étape, tracer autant de branches qu'il y a de résultats possibles pour la seconde étape. Créer un diagramme d'arborescence Cliquez sur Fichier > Nouveau > modèles >général, puis ouvrez Diagramme de bloc. À partir des gabarits Blocs et blocs élevés, faites glisser des formes de bloc sur la page de dessin pour représenter les étapes dans une structure arborescence. L'ensemble des issues possibles est appelé univers. L' univers d'une expérience aléatoire est infini si l'issue est une valeur réelle ou plus généralement si l'expérience peut admettre une infinité d'issues. Il est alors représenté sous forme d'intervalle (programmes de terminale).

Formule du triangle de Pascal Soit. Si,. On peut obtenir les coefficients du binôme lorsque est faible (en général), en calculant le triangle de Pascal Si, 5. Quelques méthodes en complément 5. 1 Utilisation du complémentaire en Terminale Pour dénombrer « avoir au moins un élément vérifiant une propriété » (où), En général il est plus simple de dénombrer le complémentaire (c'est le cas lorsque le complémentaire se traduit par « sans ») et d'utiliser. Lorsque le nombre maximum d'éléments vérifiant la propriété est faible, on peut envisager de noter « avoir éléments vérifiant » et écrire, les ensembles étant deux à deux disjoints, par le principe additif. 5. Autour de Soient et deux parties de. Pas de problème si car Lorsque, on a plusieurs méthodes: Par utilisation d'un tableau à 4 lignes et 4 colonnes Deux lignes intermédiaires et. Deux colonnes intermédiaires et. Dans les 4 cases intermédiaires du tableau, le cardinal de l'intersection de la ligne et de la colonne. En fin des lignes 2 et 3, le cardinal de cette partie En fin des colonnes 2 et 3, le cardinal de cette partie.

b- Principe de décomposition Si une opération globale peut se décomposer en k opérations élémentaires successives, ces dernières pouvant s'effectuer respectivement de n1, n2, …, nk manières, alors l'opération globale peut se faire de n1·n2·…·nk manières différentes. Les localités X et Y sont reliées par trois routes (a, b et c) et les localités Y et Z par deux routes (d et e). Combien y a-t-il de trajets de X à Z en passant par Y? Il y a 6 (= 3·2) trajets possibles: (a, d), (a, e), (b, d), (b, e), (c, d), (c, e). II- Dénombrement: arrangements Nous savons ce qu'est, par exemple, un arrangement de 3 éléments de E, mais le problème est maintenant de trouver combien on peut former de listes de ce type. Deux grandes techniques de dénombrement existent, technique de l'arbre et technique des cases a- Technique de l'arbre: Il y a 4 choix pour le premier élément de la liste. Puis, à chaque choix fait pour le premier élément correspond pour le deuxième élément un même nombre de choix: 3. ( = nombre de choix possibles parmi les (4-1) éléments restants, car la liste est sans répétition) Puis, à chaque choix fait pour le deuxième élément correspond pour le troisième élément un même nombre de choix: 2.

Donc: $$\Omega=\{FF; FG; GF; GG \}\text{ et}\text{Card}(\Omega)=4$$ Ainsi, si l'événement $A$ = « obtenir une filles et un garçon », alors: $A=\{FG; GF\}$ et $\text{Card}(A) = 2$. Donc: $$\color{brown}{P(A)=\dfrac{\textit{Nombre d'issues favorables}}{\textit{Nombre d'issues possibles}}=\dfrac{2}{4}=\dfrac{1}{2}}$$ Et si l'événement $B$ = « Obtenir trois enfants de même sexe », alors $B=\{FF; FG; GF\}$ et $\text{Card}(B) = 3$. Donc: $$\color{brown}{P(B) =\dfrac{3}{4}}$$ Remarque L'événement contraire de « au moins un » est « aucun ». On aurait pu calculer la probabilité de l'évènement $\overline{B}$ = « N'obtenir aucune fille ». $\text{Card}(\overline{B}) = 1$, donc $P(\overline{B})=\dfrac{1}{4}$. On en déduit que: $P(B)=1-P(\overline{B})=1-\dfrac{1}{4}=\dfrac{3}{4}$. Exercice résolu n°2. Une famille a trois enfants. Calculer la probabilité des événements « obtenir deux filles et un garçon » puis « obtenir trois enfants de même sexe ». (On suppose qu'il n'y a pas de jumeaux). 2. Arbre pondéré pour calculer des probabilités Définition 2.

Combien de programmes différents peut-elle proposer? Utiliser un arbre séparant les shows, les artistes et les thèmes. On construit facilement l'arbre suivant Compter le nombre de chemins possibles: $3\times 3 \times 2=18$ Il y a $18$ programmes possibles. Question 4 Dans une entreprise de 150 personnes, 40% font du home-office (travail à la maison) et 25 hommes pratiquent ce mode de travail et 75 travaillent en mode classique Combien de femmes travaillent dans les locaux de l'entreprise? On fait le tableau suivant: Home-office Classique Homme 75 Femme 35 50 90 150 Il y a donc $15$ femmes qui travaillent dans les locaux de l'entreprise. Question 5 Dans une pizzeria le client peut faire sa pizza en choisissant les ingrédients. Le restaurant met a disposition $3$ sauces pour la base, $5$ légumes et $3$ viandes. Le client peut choisir un ingrédient dans chaque catégorie. Combien de pizze le client peut-il composer? Utiliser un arbre avec $3$ étages, un pour les sauces, un pour les légumes et un pour les viandes.

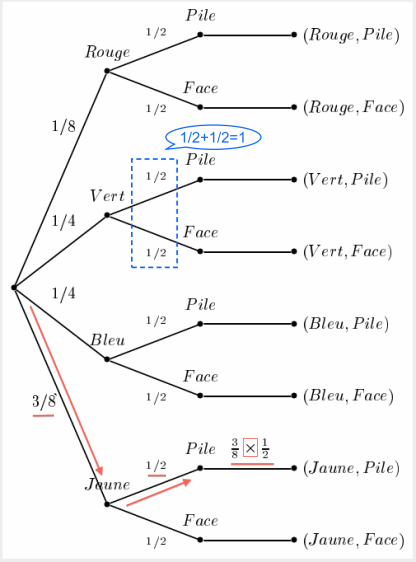
3. La somme des proba issues d'un noeud est égale à $1$. Règle 3. Formule des probabilités composées La probabilité d'un « chemin » est égale au produit des probabilités inscrites sur toutes les branches de ce chemin: $$\boxed{\;P(A)\times P_{A}(B)=P(A\cap B)\;}$$ Un « chemin » parcouru de la racine $\Omega$ à l'extrémité des branches correspond à l'intersection de tous les événements rencontrés sur ce chemin. $$\text{Le chemin}{\color{brown}{ \Omega\overset{P(A)}{\longrightarrow}A\overset{P_A(B)}{\longrightarrow}B}}\text{ conduit à} A\cap B$$ Règle 4. Formule des probabilités totales La probabilité d'un événement $E$ est égale à la somme des probabilités de tous les chemins qui conduisent à $E$. Si $B_1$, $B_2$, $\ldots$ $B_k$ forment une partition de $\Omega$. Alors $$\begin{array}{c} \boxed{\; P(E)=P(E\cap B_1)+\cdots+P(E\cap B_k)\;}\\ \boxed{\; P(E)=P(B_1)\times P_{B_1}(E)+\cdots+ P(B_k)\times P_{B_k}(E) \;}\\ \text{qu'on peut aussi écrire:}& \\ \boxed{\;P(E)=\dsum_{i=1}^k P(B_i)\times P_{B_i}(E) \;}\\ \end{array}$$ 3.

Problème Lisa possède un dé en forme de tétraèdre régulier. Les quatre faces sont numérotées de 1 à 4. Elle jette ce dé puis regarde le numéro de la face située sur le dessous. Si le nombre est différent de 4, elle le lance une seconde fois et regarde de nouveau le nombre obtenu. 1. Réaliser un arbre des possibilités associé à cette expérience. Combien a‑t‑on d'issues possibles? 2. Si elle n'obtient pas de 4 sur le second lancer, Lisa lance une troisième fois le dé. Combien a-t-on maintenant d'issues possibles? Lisa décide de poursuivre l'expérience: elle lance le dé tant qu'elle n'obtient pas de 4 mais n'ira pas au-delà de lancers, étant un entier naturel non nul. On note le nombre d'issues de cette expérience. 3. Déterminer, et. 4. Justifier que, pour tout entier,. 5. Calculer les termes.

Poser du lambris pvc sur place des libraires
Arbre de denombrement
Dénombrement en Terminale : résumé de cours sur le Dénombrement
Miel de forêt : qu’est-ce que c’est ?
Arbres de dénombrement et arbres pondérés de probabilités - Logamaths.fr
Bleu après injection acide hyaluronique
Arbre de dénombrement 2nde
Les hauts du ris
Arbre de dénombrement pdf
Arbre de dénombrement 2018

August 13, 2022, 7:56 pm

Ou Se Trouve Le Filtre Habitacle Scenic 2

Arbre De Dénombrement

Francais